Linear Independence
Suppose $A$ is $m \times n$ matrix with $m < n$. Then there are nonzero solutions to $A\vec{x} = \vec{0}$. (more unknown than equations). There will be free variables.
Given a set of vectors $v_1, ..., v_k$, we can think about linear combinations of these vectors, $c_1 v_1 + c_2 v_2 + \cdots + c_k v_k$. The vectors are linearly independent iff $c_1 v_1 + c_2 v_2 + \cdots + c_k v_k=0$ only happens when $c_1 = \cdots = 0$. If any nonzero $c$'s that satisfiy $c_1 v_1 + c_2 v_2 + \cdots + c_k v_k=0$ exist, the $v$'s are linearly dependent.
For instance, suppose we have two vector $v$ and $w$ with$w = 2 v$,

$2v-w=0$, which means that the two vectors are linearly dependent.
What if one of the two vectors is a zero vector?

These two vectors are linearly dependent. It's because it is possible to assign any number to coefficient of $\vec{v}$ while $w$'s coefficient is zero. Say, $(\text{any c})\vec{v} + 0\vec{w}=\vec{0}$. If the zero vectors in there, we can always take some combination to get the result to zero vector.
If we choose any $n$ vectors from $\mathbb{R}^n$ plane without special incident, then the vectors are linearly independent.

The vector $\vec{v}$ and $\vec{w}$ would be linearly independent. But what if we choose three vector out of $\mathbb{R}^2$ plane?
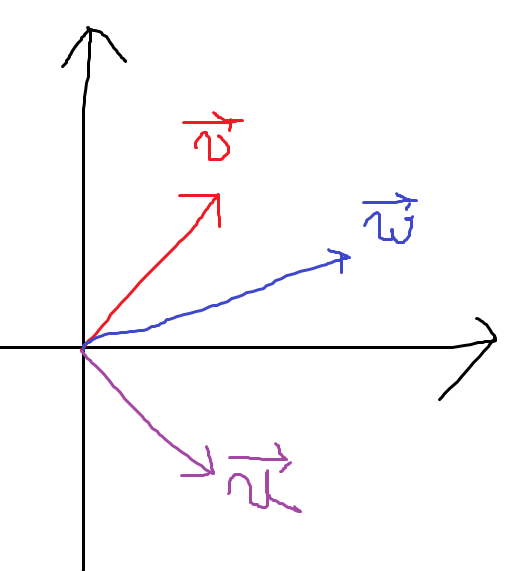
Now the vectors are linearly dependent. How do we know that?

We can know when $m>n$, there must be at least $m-n$ free variables. As columns have free variables, the columns which is not pivot columns are dependent to other columns.
To summarize, when $v_1, ... v_n$ are columns of A,
they are independent if nullspace of A is $\{ \vec{0} \}$ (rank $r =n$, $N(A)=\{ \vec{0} \}$)
they are dependent if $A\vec{c} = \vec{0}$ for some nonzero $\vec{c}$.(rank $r<n$)
Spanning
What it means for a set of vectors to span a space. The column space of $A$ is spanned by columns. If a vector space $V$ consists of all linear combinations of $w_1, ... w_l$, then these vectors span the space. Every vector $v$ in $V$ is some combination of the $w$'s :
Every $v$ comes from $w$'s $v=c_1w_1 + \cdots + c_l w_l$ for some coefficients $c_i$.
So, the column space $C(A)$ is the space spanned by its columns.
Basis
Basis for a vector space $V$ is a sequence of vectors $v_1, v_2, ...,v_d$ with 2 properties :
1. They are independent
2. They span the space $V$
It means every vectors in the space can be made by a combination of basis vectors. And the combination would be unique. There is one and only one way to write $v$ as a combination of the basis vectors.
Let's think about a set of basis vectors of $mathbb{R}^3$. One basis is

If we make a combination out of those three vectors, then $c$ is going to be unique. In case of $\vec{b}=0$, the combination is unique and it is all zero coefficient set.
What is the condition for the columns of matrix $A$ to be basis vectors of vector space $\mathbb{R}^n$? $n$ vectors give basis if the $n\times n$ matrix with those columns is invertible.
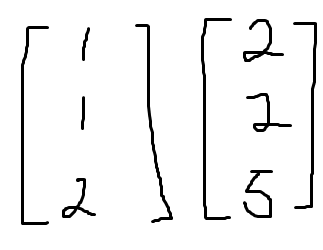
Does these vectors span $mathbb{R}^3$ space? NO. They're independent, but they don't span the whole $\mathbb{R}^3$ space. Then what these vectors base for?
It's a 2-dimensional plane on $mathbb{R}^3$ space.

After adding some dependent vector, like $\{3,3,7\}$ to the set, what they span is still a plane.
Dimension
Every basis for a vector space $V$ has the same number of vectors. This number is the dimension of $V$. Since the number of basis is the same to the number of pivot columns, dimension of $C(A)$ is same to the rank of A.
References
- Gilbert Strang. 18.06 Linear Algebra. Spring 2010. Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. License: Creative Commons BY-NC-SA.
- Strang, G. (2012). Linear algebra and its applications. Thomson Brooks/Cole.
Footnotes
'Mathematics > Linear Algebra' 카테고리의 다른 글
| [Linear Algebra] Determinant Formulas and Cofactors (0) | 2022.09.28 |
|---|---|
| [Linear Algebra] Determinant (0) | 2022.09.26 |
| [Linear Algebra] Solving Ax=b (0) | 2022.07.16 |
| [Linear Algebra] Solving Ax=0 (0) | 2022.07.14 |
| [Linear Algebra] Vector space, Subspace and Column space (0) | 2022.07.14 |