Solving Ax=0
Suppose we have a square, invertible matrix $A$. It is supposed to have $n$ pivots in $n$ columns. But what if we have rectangular matrix that may not have full set of pivots? let's think about a rectangular matrix $A$ and a corresponding linear system $A\vec{x}=\vec{0}$.

We can do Gaussian elimination on this matrix $A$ and get $U$.

Since the third row is a sum of the first and second row, it becomes all zero after doing elimination. As we can see, we have a upper triangular matrix $U$, but it is somewhat different to standard form as its pivots are not on the main diagonal. The nonzero entries of U have a "staircase pattern", or echelon form. And we define the numbers of pivots as rank. In this case, the rank of the matrix $A$ in 2.
Reduced Row Echelon Form
We can do more with echelon matrix $U$. By subtracting pivot row from above rows to produce all zero entries above the pivot, and multiplying proper constants to pivots to make them all one, we can get a new matrix that is a reduced row echelon form $R$.

The reduced row echelon form of a square invertible matrix is identity matrix. In our case, $R$ still has an identity matrix in its pivot columns.

Pivot Variables and Free Variables
And this identity matrix is multiplied with $x_1$ and $x_3$.

This group of variables are pivot variables that correspond to columns with pivots. What about left columns?

The second and forth columns are multiplied with $x_2$ and $x_4$. This group of variables are free variables that correspond to columns without pivots.
To find the most general solution to $R\vec{x}=\vec{0}$, we can assign any number to these free variables and then the values of pivot variables are determined systemically. Say, if $x_2 =1$ and $x_4=0$, then by the following equations,

$x_1$ is determined to -2, and $x_3$ is determined to 0. Similarly, we can get another special solution by substiting 0 and 1 for $x_2$ and $x_4$, respectively.
Then, what are the all solutions of this system? The complete solution is a combination of two special solutions.

How many special solutions are there? There must be at least $n-m$ free variables. There will be even more free variables if some rows of $R$ reduce to zero : There are more than the trivial $x=0$. The nullspace has the same "dimension" as the number of free variables and special solutions. The idea of the dimension of a subspace is made precise in following session.
In short, we can find All solutions by following steps :
1. After reaching $R\vec{x}=\vec{0}$, identify the pivot variables and free variables.
2. Give one free variable the value 1, set the other free variables to 0, and solve $R\vec{x}=\vec{0}$ for the pivot variable. This is the special solution.
3. Every free variables produces its own "special solution". The combinations of special solutions form the nullspace.
Representing the solutions with matrices
Suppose a typical form that pivot columns are on the left side and free columns on the right side, the matrix is going to be as:
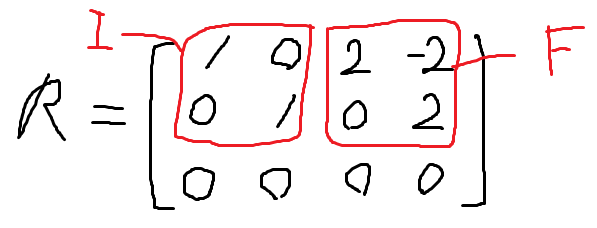
It can be represented in simple form with $r$ pivot columns and $n-r$ free columns:

Solution of this matrix is going to be :

From $\vec{x}$'s features, we can draw this conclusion :

It can be demonstrated by this example :

References
- Gilbert Strang. 18.06 Linear Algebra. Spring 2010. Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. License: Creative Commons BY-NC-SA.
- Strang, G. (2012). Linear algebra and its applications. Thomson Brooks/Cole.
Footnotes
'Mathematics > Linear Algebra' 카테고리의 다른 글
| [Linear Algebra] Linear Independence, Basis and Dimension (0) | 2022.07.20 |
|---|---|
| [Linear Algebra] Solving Ax=b (0) | 2022.07.16 |
| [Linear Algebra] Vector space, Subspace and Column space (0) | 2022.07.14 |
| [Linear Algebra] LU Factorization (0) | 2021.12.29 |
| [Linear Algebra] Matrix Multiplication의 이해 (0) | 2021.12.28 |