Solving Ax=b, Ux=c, and Rx=d
Unlike last time, suppose we have a linear system that have non-zero right-hand-side. The case $b \neq 0$ is quite different from $b = 0$. Right hand side terms will be changed as we do elimination process on left hand side. Let's think we have a linear system like below :

This whole system can be represented as an augmented matrix form $\left[A|\vec{b}\right]$ - which is a notation of a matrix that right hand side $b$ is tagged on :

By using Guassian elimination, the matrix $A$ can be reduced to echelon form $U$. As $A$ is reduced, $\vec{b}$ is also changed to another vector. It is not $\vec{b}$. So the result is $U\vec{x} = \vec{c}$.

Suppose we have $b=(1, 5, 6)$, then it is going to be like :

Solvability Condition on $\vec{b}$
When does it have solution? The equations are inconsistent unless $b_3 - b_2 - b_1 = 0$. If a combination of rows of $A$ gives zero row, then the same combination of the entries of $\vec{b}$ must give $0$.
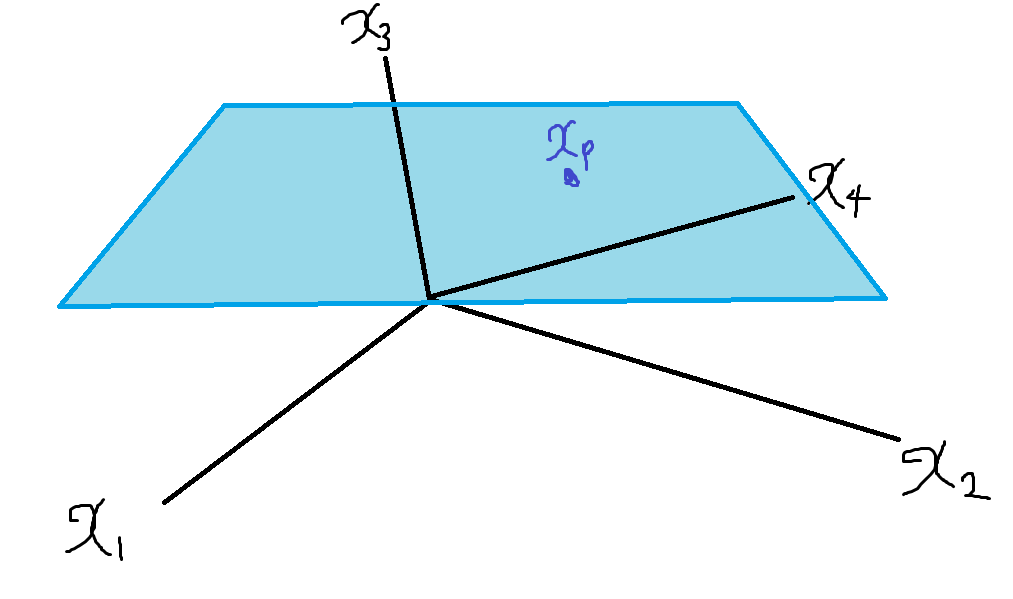
Another way to answer this is that, $A \vec{x} = \vec{b}$ is solvable iff b is in $C(A)$.(not U) How $C(A)$ seems like? Even though there are four vectors, since the second and fourth columns are dependent, it is the plane generated by columns 1 and 3.
Complete Solution of $A\vec{x} = \vec{b}$
To find complete solution to $A\vec{x} = \vec{b}$, we assign all 0 to free variables to matrix $A$ or $U$ or $R$. For a specific example with $b_3 - b_2 - b_1 = 0$, choose $b=(1, 5, 6)$.

Then $x_1 = -2$, $x_3 = {3 \over 2}$, and whole $\vec{x}$ is :

It is a particular solution of $A \vec{x} = \vec{b}$, and if we add any vector $\vec{v}$ in the nullspace, the equation $A(\vec{x} + \vec{v}) = 0$ is still satisfied. Since there are infinity of solutions per every single free variables, every solution $A \vec{x} = \vec{b}$ is the sum of one particular solution and a solution to $A\vec{x} = \vec{0}$.
$$ x_{complete} = x_{particular} + x_{nullspace}$$
In above's case, $x_{complete}$ is :

Geometrically, the solutions again fill a two-dimensional plane, but as it does not contain $\vec{x}=\vec{0}$, it is not a subspace. It is parallel to the nullspace we had before, shifted by the particular solution $x_p$.
What is the advantage to use reduced row echelon form in the process of finding complete solution of a linear system? It can seen in an example of $R\vec{x} = \vec{d}$.

To find the particular solution, $v=y=0$, so columns 2 and 4 can be ignored. Then the entries of $d$ go directly into $x_p$.
Solutions and Rank
If there are $r$ pivots, there are $r$ pivot variables and $n-r$ free variables. $r$ is called as a rank of the matrix. Let's see how can we determine the number of solutions by $r$,$m$,$n$.
$r=m=n$
In this case, $A$ is an invertible square matrix. It's reduced row echelon form is $R=I$. All the columns of $A$ are independent, so they span the whole $\mathbb{R}^n$ vector space. Therefore, $A\vec{x}=\vec{b}$ has only one solution regardless of the value of $\vec{b}$.
$r=n<m$
Reduced row echelon form of $A$ is

, and it has 0(when the 0 rows are inconsistent) or 1 solution(rows are consistent).
$r=m<n$
Reduced row echelon form of $A$ is
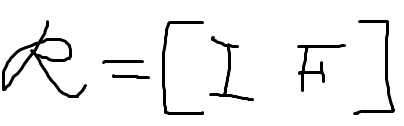
, and it has 1 or $\infty$ solutions. If its nullspace contains zero vector only, then the number of solutions will be 1. $\infty$ otherwise.
$r<m$, $r<n$
Reduced row echelon form of $A$ is

It has 0 or $\infty$ solutions. If the last row is inconsistent, this system has no solution. On the other hand, if the last row is consistent, then we can assign any number to last $m-r$ variables, so the number of solution is infinite.
References
- Gilbert Strang. 18.06 Linear Algebra. Spring 2010. Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. License: Creative Commons BY-NC-SA.
- Strang, G. (2012). Linear algebra and its applications. Thomson Brooks/Cole.
Footnotes
'Mathematics > Linear Algebra' 카테고리의 다른 글
| [Linear Algebra] Determinant (0) | 2022.09.26 |
|---|---|
| [Linear Algebra] Linear Independence, Basis and Dimension (0) | 2022.07.20 |
| [Linear Algebra] Solving Ax=0 (0) | 2022.07.14 |
| [Linear Algebra] Vector space, Subspace and Column space (0) | 2022.07.14 |
| [Linear Algebra] LU Factorization (0) | 2021.12.29 |