Adversarial Attack

Introduction

Adversarial attack은 machine learning algorithm이 올바르지 않은 행동을 하도록 만드는 공격을 의미한다. 특히 Deep neural network의 경우에는 adversarial attack에 대해 vulnerable하다고 알려져 있는데, 각종 핵심 기능에 사용되는 DNN 모델의 특성 상 security가 강하게 요구된다. 따라서 이를 방어하는 방법을 adversarial defense라고 하고 이 모든 분야를 합쳐 adversarial machine learning이라고 한다. 

 

처음 이 vulnerability가 제안된 것은 Szegdy et al.[2] 의 dnn에서의 image classification task이다. image에 target class로 모델이 classify하도록 perturbation을 original sample에 더하면 사람의 눈에는 detectable하지 않지만 모델은 high confidence로 target label로 착각한다. (See Fig. 1)

Figure 1: Adversarial example generation process[1].

 

전체 공격 process는 Fig. 2와 같이 표현된다.

Figure 2: Adversarial example generation and adversarial attack process.

 

이외 몇 가지 term은 다음과 같다:

• black-box attack: attacker가 deep neural network의 model structure와 parameter에 access할 수 없는 경우의 공격.
• white-box attack: attacker가 dnn의 structure와 parameter를 가지고 있는 경우의 공격.
• one-shot attack: 한 번의 calculation으로 high attack success rate를 달성할 수 있는 경우.
• iterative attack: multiple time의 algorithm iteration을 통해서 공격하는 경우.
• targeted attack: target model이 공격 당한 뒤 specific classification result를 내도록 유도되는 경우.
• non-targeted attack: 목표하는 classification result에 제한을 두지 않는 경우.
• specific perturbation: 각 input original data에 다른 perturbation이 적용되는 경우.
• universal perturbation: 모든 input original data에 동일한 perturbation이 적용되는 경우. 

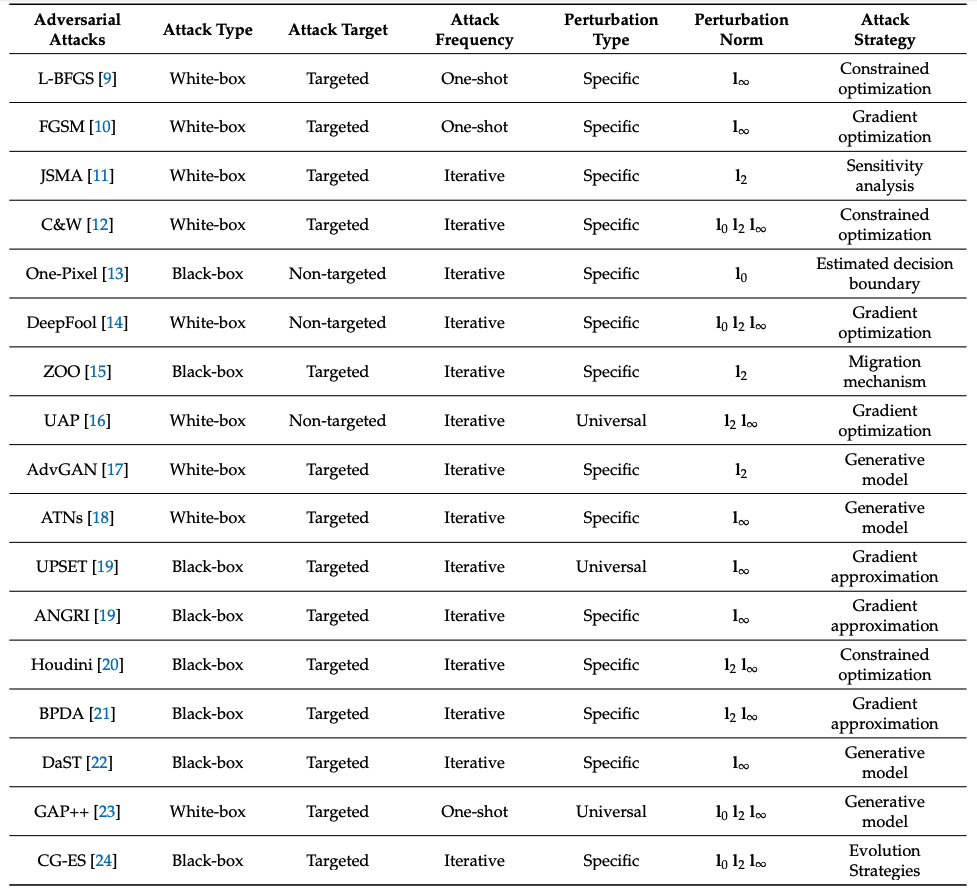
이 기준에 따라 Tab. 1과 같이 전형적인 adversarial attack들을 분류할 수 있다:

 

Table 1: Summary of typical adversarial attack and its principle [1].

 

Fast Gradient Sign Method(FGSM)

FGSM은 Goodfellow et al. [3]에 의해 제안되었다. 이는 dnn의 vulnerability가 high-dimensional linearity로 인해 발생함을 증명한 것이다. 이 방법은 deep learning model의 maximum direction of gradient change로 perturbation을 만들어 adversarial sample을 만든다. 이는 다음과 같이 표현될 수 있다:

 

$$ δ = ε \text{sign} (\nabla_x J_θ (θ, x, y))$$

 

δ는 generated perturbation, y는 target, $J_θ$는 loss function, ε는 constant를 의미한다. 

 

FGSM에 대한 자세한 내용은 이 포스트에서 다룬다. 

 

---

Adversarial Defense

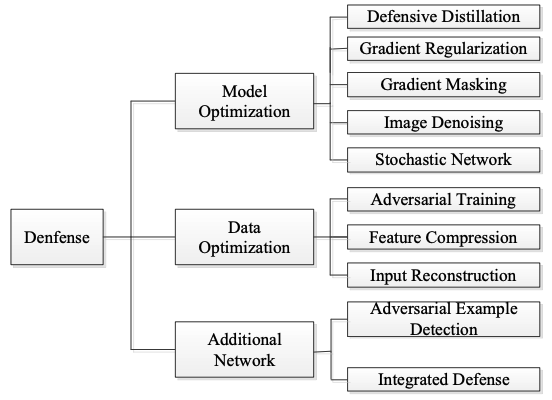
Szegedy et al.[2] 는 real data 안에도 낮은 확률로 adversarial sample이 존재하지만 그 빈도가 낮아 train하기가 어렵다고 보았다. 따라서 이를 명시적으로 train하는 방법 등으로 공격을 방어할 수 있다. Defense의 방법은 다음과 같이 나눌 수 있다:

 

Figure 3: Adversarial attack defense methods of dnn. [1]

 

 

 

---

References

[1] Liang, H., He, E., Zhao, Y., Jia, Z., & Li, H. (2022). Adversarial attack and defense: A survey. Electronics, 11(8), 1283. https://doi.org/10.3390/electronics11081283

[2] Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. arXiv 2013, arXiv:1312.6199

[3] Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and Harnessing Adversarial Examples. arXiv 2014, arXiv:1412.6572.

 

Footnotes