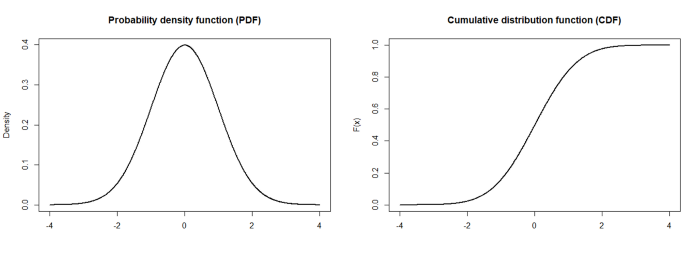
IntroductionK-S test는 두 가지 경우에 사용된다. 첫 번째는 추출한 샘플들이 특정한 probability distribution을 따를 것인지를 확인하는 것이고(one-sample K-S test), 두 번째는 두 개의 sample 집합을 보고 같은 probability distribution에서 추출되었는지를 확인하는 것이다(two-sample K-S test). K-S test는 non-parametric test이다. 두 함수가 continuous한 경우나 discrete한 경우 모두 사용할 수 있다. continuous한 경우에는 CDF(cumulative distribution function)을 사용하고, discrete한 경우에는 EDF(Empirical distributio..

Guassian elimination와 upper triangular matrix non-singular $3 \times 3$ matrix $A$가 row exchange없이 upper-triangular matrix $U$로 변환 가능하다고 하자. 예를 들어 다음의 matrix $A$가 있다. $$ A = \begin{bmatrix} 2 & 1 &1 \\ 4 & 3 & 7 \\ -2 &1 & 3 \end {bmatrix} $$ 이 matrix에 대한 equation $Ax=b$가 다음과 같다. $$\begin{align} Ax &= b\\ \begin{bmatrix} 2 & 1 &1 \\ 4 & 3 & 7 \\ -2 &1 & 3 \end {bmatrix} \begin{bmatrix}u \\v\\w \..

Matrix Multiplication 두 matrix $A$, $B$를 곱하는 상황을 생각해 보자. 이때 matrix $A$는 $2 \times 2$ 인 square matrix이고, $B$는 $2 \times 3$인 rectangular matrix이라고 하자. 즉, 다음과 같다. $$ A = \begin{bmatrix} 2 & 3 \\ 4 & 0 \end{bmatrix} \text {, } B = \begin{bmatrix} 1 & 2 & 0 \\ 5 & 1 & 0 \end{bmatrix}$$ 이때 두 matrix의 multiplication은 다음과 같이 될 것이다. $$ AB = \begin{bmatrix} 2 & 3 \\ 4 & 0 \end{bmatrix} \begin{bmatrix} 1 & ..

Introduction 두 개의 equation과 두 개의 unknown이 있는 system을 예로 들어보자. $$ 2x - y = 0 \\ -x + 2y =3 $$ 이 system은 coefficient matrix $A$와 column vector $\bf{x}$, column vector $\bf{b}$로 나타낼 수 있다. $$ \begin{bmatrix} 2 & -1 \\ -1 & 2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 3 \end{bmatrix}$$ $$ A \bf{x} = \bf{b} $$ Row picture Row picture의 개념은 위 system을 row 방향으로 쪼개서 n개의 n-dim..

적률(Moment)란 Random Variable X의 n승의 expectation을 의미한다. 예를 들어 X의 1차 적률은 E(X), 2차 적률은 E(X^2) 이런 식이다. 이런 적률을 생성하는 함수로서, 다음과 같다. 이 적률생성함수를 n번 미분하여 t=0을 대입하면 X의 n차 적률을 구할 수 있다. 증명 e^(tx)는 테일러 전개에 의해 다음과 같이 표현될 수 있다. a=0을 대입하면 다음과 같다.(매클로린 급수) 양변의 expectation은 다음과 같다. 이 식의 양변을 n번 미분하고 t=0을 대입하면 적률을 구할 수 있다. 다음 예를 보자. 위와 같이 한 번 미분한 식에 t=0을 대입하면, 이를 일반화하면 다음과 같다. Continuous PDF의 경우 적분으로 expectation을 구할 수..

Taylor series는 함수를 한 점에서의 derivatives들의 무한 개의 항의 합으로 근사하는 방법이다. 일반적으로 이 점에서 두taylor function과 원래 함수는 어느 정도 근사한다. 유도 테일러 함수는 미적분의 기본 정리로부터 간단히 유도할 수 있다. 먼저 미적분의 기본정리 식을 f(x)에 대해 정리하고, f'(t)의 정적분항을 1과 f'(t)로 부분적분한다. 이때 적분상수는 C로 둔다. 적분상수를 -x로 대입하고, 뒤 정적분식을 다시 부분적분하면 다음과 같이 정리할 수 있다. 이러한 과정을 반복하면 다음과 같다. 이를 간단하게 쓰면 다음과 같다. 이를 테일러 급수(Taylor series)라고 한다. 또한 a=0인 특수한 경우에 식은 다음과 같이 표현되는데, 이러한 형태를 매클로린 ..