논문에 언급된 내용이 아닌 주관적인 생각은 파란색으로 표기하였습니다.
Abstract
- 왜 random initialization을 사용하는 gradient descent가 deep neural network에서 저조한 결과가 나오는지 알아본다.
- non-linear activation function이 각각 학습에 어떤 영향을 미치는지 알아본다.
- 이 연구에서, sigmoid activation은 random initialization을 사용하는 DNN에 unsuit함을 알아낸다.
- 덜 saturate하는 새로운 non-linearity(softsign activation)가 학습에 유의미한 성과를 가져옴을 보여주었다.
- activation과 gradient가 layer별로 어떻게 변화하는지 살펴보았다.
- 훨씬 더 빠른 convergence를 가져오는 새로운 initialization 방법을 제안한다. (Xavier initializer)
- 단, ReLU function이 개발된 이후에는 softsign이나 sigmoid, tanh는 잘 사용하고 있지 않아서, activation function에 집중하는 것은 현재로서는 큰 의미가 있는 것은 아닌 것으로 생각된다. 하지만 Xavier intializer라는 새로운 initialization scheme이 paper에서 'normalized initialization'라는 이름으로 제안되는데, 이 방법은 오늘까지도 모델의 performance를 향상시키기 위한 방법으로 사용되고 있다.
Introduction
선행연구와 연구개요
2010년도까지 이루어진 연구들을 살펴보면, 고차원적으로 추상화된 데이터의 복잡한 feature를 학습하기 위해서는 deep architecture가 반드시 필요한 것으로 생각된다. 하지만 deep architecture의 학습은 2010년 기준 최근에 들어서야 그 성과가 나타나기 시작했는데, 이는 gradient based learning에서 unsupervised pretraining 덕분이라고 언급된다. 왜냐면 unsupervised pretraining이 generalization의 성능을 향상시키는 regularizaer로서의 기능을 했기 때문이다. (Erhan et al., 2009) 그러나 이전 연구에서는 purely supervised but greedy layer-wise procedure이 더 나은 결과를 보여주기도 하였다.(Bengio et al., 2007)
하지만 이 논문에서는 그러한 것에 집중하지 않고, 전통적인 multi-layer neural network를 분석한다. 이 분석은 layer와 training iteraion이 진행됨에 따라 gradient와 activation 값이 어떻게 변화하는지를 지켜보면서 분석한다.
- unsupervised pretraining과 greedy layer-wise procedure 역시도 모델의 depth가 깊어질 수록 gradient가 죽는 문제를 해결하기 위해서 사용되었던 방법이다. ReLU 이후로는 잘 사용되지 않는다.
Datasets
여기서는 두 종류의 dataset을 사용한다.하나는 Larochelle et al.(2007)에서 영향을 받은 synthetic image이다. 이 dataset은 Shapeset-3×2라고 이름 붙여졌는데, 2차원 도형(삼각형, 평행사변형, 타원)이 1-2개 나타나는 흑백 이미지이다.

실제 학습에서는 32×32로 조정하여 사용하였고, 도형들이 여러 rotation, translation을 비롯한 여러 variation이 있으므로 어떤 도형이 나타나는지 판단하는 것은 꽤 어려운 문제이다.
두 번째 dataset은 Small-ImageNet인데 이는, 37×37 크기의 회색 이미지들이다. 90,000개의 training set과 10,000개의 validation set, 10,000개의 test set을 이용했고 10개의 class가 balanced하게 label되어 있다.

실험 세팅
1-5개의 hidden layer를 사용하는 feedforward neural network를 사용하였다. 각 layer에는 1,000개의 unit이 있고, output layer는 softmax logistic regression을 사용한다. Shapeset에서는 모두 5개의 layer를 사용하였고, sigmoid에서만 5개 layer 사용 시 학습이 아예 이루어지지 않으므로 4개의 layer를 사용하였다.
cost function은 negative log-likelihood $-\log P(y|x)$를 사용한다. batch size는 10이고, stochastic gradient descent로 backpropagation한다.
사용한 activation function은 sigmoid, tanh, softsign이다.
initialziation은 다음과 같다 :
$$ W_{ij} \sim U \left [ - {1 \over \sqrt{n}}, {1 \over \sqrt{n}} \right ] $$
이때 $U$는 uniform distribution을 의미하고, $n$은 이전 layer의 size를 의미한다.
Results
sigmoid에서의 결과
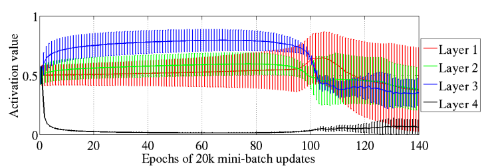
위 Figure 2가 sigmoid activation으로 Shapeset을 학습할 때의 결과이다. 총 4개의 layer를 사용했고, horizontal line은 activation value를 보여주고, vertical line은 그 layer의 activation 값들의 standard deviation을 보여주는 것이다.
주목할 점은, 거의 학습을 시작하자마자 layer 4의 activation value는 0에 가깝게 떨어져 saturated된다는 점이다. 이러한 saturation은 거의 epoch 100까지 이어지다가, epoch 100이 지나면서 서서히 해소된다. 이 때 동시에 layer 1, 2, 3에서는 activation value가 점차 떨어져 전체적으로 stabilize하는 것으로 볼 수 있다.
paper에서는 이것이 random initialization 떄문일 것으로 추측한다. 즉, output layer $\text{softmax} (b+Wh)$는 초반에 random하게 initialized된 $Wh$가 not useful하다고 보고 bias $b$에 더 의존하게 된다는 것이다. 이 방식은 점점 $h$를 0으로 수렴하도록 만들고, 결과적으로는 staturation을 만들게 된다.
Hyperbolic tangent에서의 결과
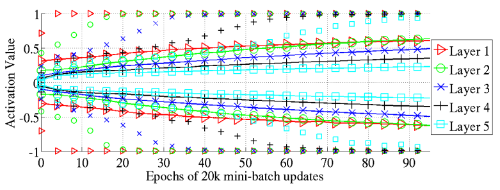
tanh에서는 sigmoid같은 현저한 saturation이 나타나지는 않았다. 대신 다른 형태의 saturation이 발견되었는데, Figure 3 Top을 보면 독립적인 mark로 상위와 하위 98% percentile의 activation value가 나타나 있고, solid line으로는 standard deviation이 나타나 있다.
이를 보면, 시작하자마자 layer 1에서 saturation이 발생하고 뒤이어 layer 2, layer 3에서 연쇄적으로 saturation이 발생하는 것을 볼 수 있다. 또한 saturation이 이미 발생한 layer의 경우에도 점점 saturated된 unit의 개수가 증가하는 것을 볼 수 있다. 논문에서 이 현상의 원인은 설명하지 않는다.
- 98 percentile의 activation 값이 1에 박혀있다는 것은 아주 강하게 saturated되어 있는 것을 의미한다. 거의 학습이 되지 않고 있는 상황이다. 98 percentile하고 standard deviation만 그려져 있어 정확히 어떻게 변화하는지는 알 수 없지만, standard deviation의 증가는 양 극단에 있는 값, 즉 saturated unit의 개수가 증가하는 것으로 생각할 수 있다. 이는 Figure 4에서도 비슷한 결과로 뒷받침된다.

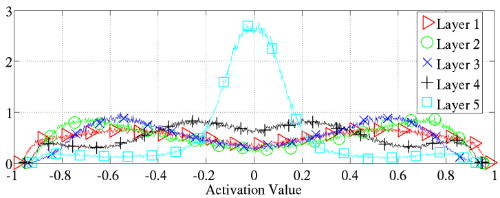
Figure 4 Top은 학습이 모두 종료된 후에 layer 별로 activation value의 distrubution을 histogram으로 보여 준 것이다. lower layer에서 더 강한 saturation을 볼 수 있다.
- 여기서 집중해야 하는 값은 -1과 1 근방이다. 실제로 layer 1이나 layer 2에서 variance가 훨씬 크고, 또 양 극단의 값이 크게 치솟아 있는 것을 볼 수 있다. 상당한 saturation을 겪었다는 뜻이다.
Softsign에서의 결과
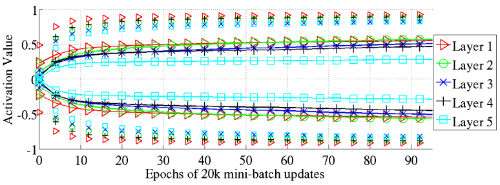
softsign에서는 tanh에서 보였던 saturation도 보이지 않는다. 대부분의 값이 0.6-0.8 사이에 있는 것을 볼 수 있다. 이는 saturated되지 않았을 뿐 아니라 non-linearity가 살아있는 구간이다.
이 Figure에서도 양 끝 값을 보면 거의 saturated되지 않았음을 확인할 수 있다.
- 참조하기 위해 softsign 그래프를 보여주자면 다음과 같다 :
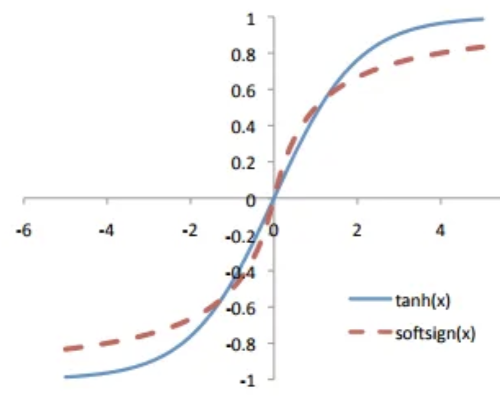
$f(x) = {x \over { |x| +1}}$의 그래프인데, asymtote를 1과 -1에서 가진다는 점은 동일하지만, 더 늦게 수렴한다. 따라서 saturated되는 구간도 더 좁을 수 밖에 없다. 이런 점을 이용한 것이다.
Cost function의 효과
negative log likelihood는 cross entropy에 비해 plateau가 적으므로 학습에 용이하다.
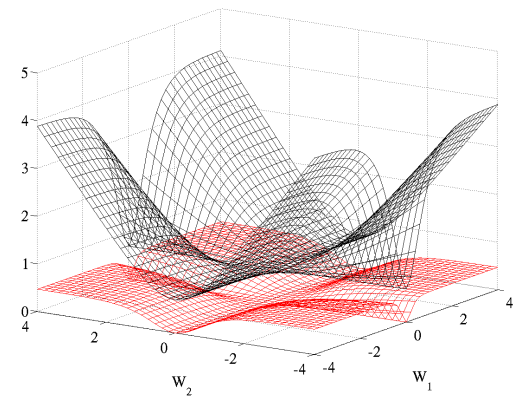
흑색 그래프가 negative log likelihood이고, 적색 그래프가 cross entropy이다. 한 눈에 보기에도 saddle point가 적음을 확인할 수 있다.
- 논문에서 plateau라는 표현이 자주 등장하는데, 이는 local optima와 saddle point와 같이 학습을 지체시키는 loss function의 지형을 가리키는 것이다.
New normalized intialization (Xaiver initialization)
실제로 Bradley(2009)에 따르면, back-propagated gradient는 layer가 지날 수록 점점 작아지는데, back-propagated gradient의 variance도 감소하게 된다. 따라서 backpropagated gradient와 activation의 variance를 모든 layer에서 일정하게 유지시킬 수 있는 새로운 initialization 기법을 제시한다.
이를 normalized initialization이라고 하고, 다음과 같다 :
$$ W \sim U \left [ - {\sqrt{6} \over \sqrt {n_j + n_{j+1}}}, {\sqrt{6} \over \sqrt {n_j + n_{j+1}}} \right ] $$
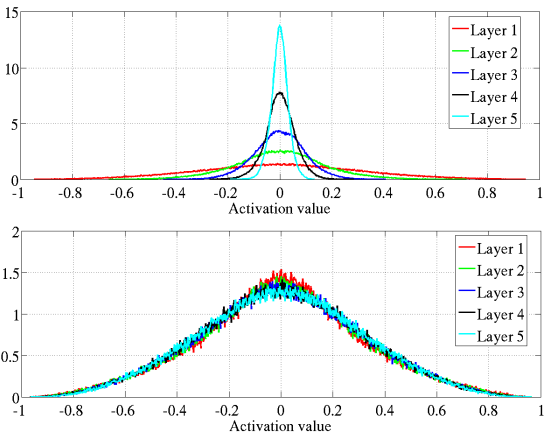
Figure 6는 tanh activation의 각 layer별 activation value들이다. 두 그래프의 차이점은 위는 standard initialization를 사용한 것이고 아래는 normalized initialization (Xavier initialization)을 사용한 것이다. 한 눈에 보기에도 모든 layer에서 variance가 일정하게 유지되었음을 확인할 수 있다.
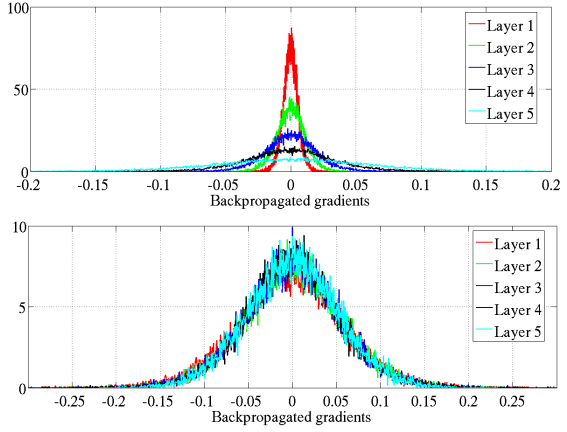
Figure 7은 같은 조건에서의 back-propagated gradient를 보여주는 것이다. 역시 variance가 일정하게 유지됨을 확인할 수 있다.
- 특히 Figure 6과 Figure 7은 x scale과 y scale이 달라지므로 이 점에 유의해서 보면 좋다. 원래 tanh network에서, 대부분의 activation이 뒤로 갈 수록 점점 작아지고, 역전파값은 그 반대로 받고 있었다. 앞쪽 layer의 학습이 잘 되지 않고 있었다고 볼 수 있다.
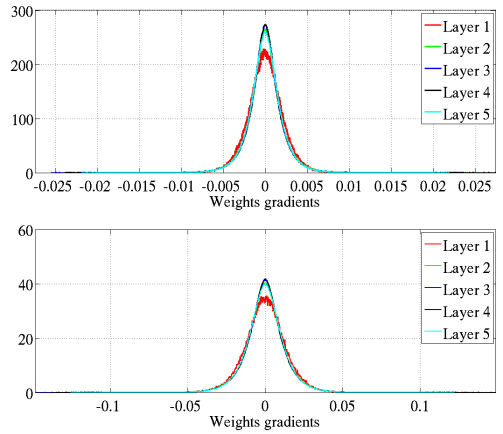
Figure 8은 weight gradient의 histogram이다. Figure 7의 결과와는 다르게 standard intialization을 사용하는 경우에도 layer가 지나면서 gradient가 죽지 않는다.
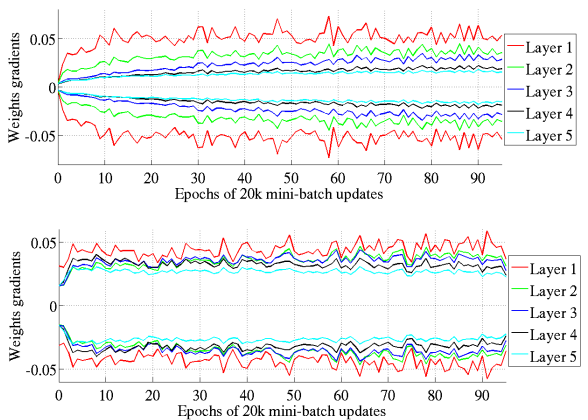
Figure 9는 tanh를 사용하는 경우 weight gradient의 standard deviation가 학습의 진행에 따라서 변화하는 모습을 보여주는 그래프이다. 위는 standard initialization을 사용한 것이고 아래는 normalized initialization을 사용한 것이다. 학습을 진행하면서 standard initialization에서는 점점 standard deviation이 증가하지만, normalized initialization을 사용하는 경우에는 standard deviation이 거의 constant하게 나타난다.
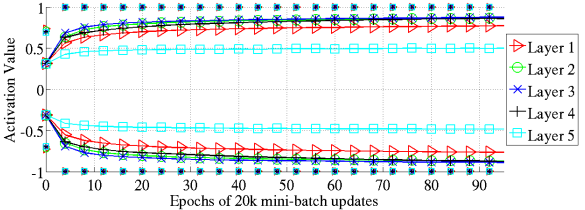
Figure 10은 normalized initialization scheme을 사용하는 tanh의 98 percentile와 standard deviation 그래프이다. softsign의 figure과 비슷한 양상을 보여준다.
Conclusion
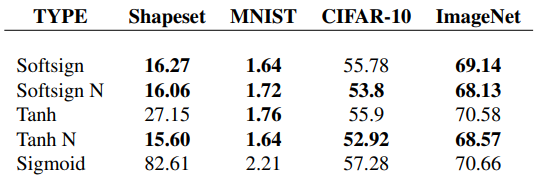
Table 1은 각 데이터셋에서의 test error 값이다. 뒤에 N이 붙은 것은 normalized intialization scheme을 사용했음을 나타낸다. 볼드체로 표현된 수는 non-bold인 수와 유의하게 다름을 나타낸다. 특히 tanh activation을 사용하는 경우 normalized initialization scheme이 큰 향상을 가져옴을 알 수 있다.
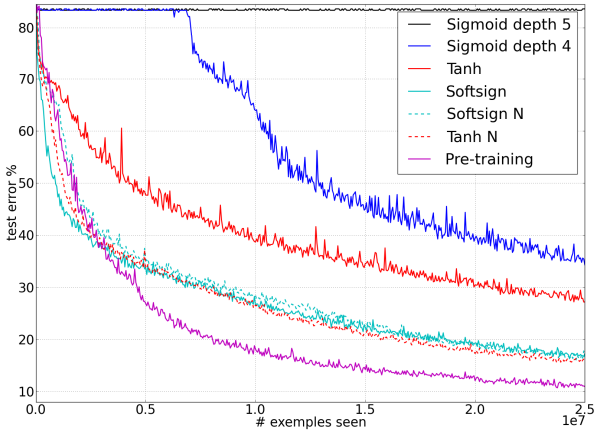
Shapeset-3×2를 사용한 경우의 online training의 test error이다.
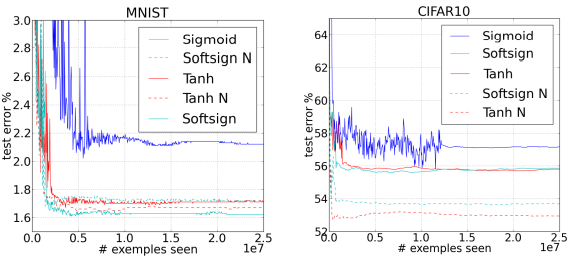
MNIST와 CIFAR-10에서의 training 중 test error curve이다.
여기서 다음과 같은 결론들을 얻을 수 있다 :
- 기존의 전통적인 tanh와 sigmoid를 사용하는 neural network는 더 느리게 수렴하고, 결과도 나쁘다.
- sigmoid activation은 사용하지 말아야 한다.
- softsign network는 좀 더 robust한 경향성이 있다.
- tanh activation에서 normalized initialization은 성과를 향상시킨다.
- layer간 transformation에서 varinace를 유지하는 것은 도움이 된다.
References
X. Glorot and Y. Bengio. Understanding the difficulty of training deep feedforward neural networks. In Aistats, volume 9, pages 249–256, 2010. 5
'DL·ML' 카테고리의 다른 글
| [DL] Hierarchical Softmax (0) | 2022.07.01 |
|---|---|
| [ML] Reduced Error Pruning (0) | 2022.03.18 |
| [DL] RNN(Recursive Neural Network)의 이해 (0) | 2021.12.26 |
| [paper review] ImageNet Classification with Deep Convolutional Neural Network (AlexNet) (0) | 2021.11.29 |
| 경사하강법(Gradient Descent) (0) | 2021.06.21 |