* 원 논문에서의 Figure 번호는 괄호 안에 표기하였습니다.
1. Motivation
ChatGPT나 GPT4 같은 모델을 보면, 복잡한 task에서는 좋은 성능을 보이지만 오히려 3자리 수 곱셈과 같은 간단한 task에서 fail하는 경우가 많다. 이 논문에서는 multi-hop reasoning을 통해 정답을 도출해야 하는 task를 compositional problem이라고 명명하고, 이를 통해 Transformer architecture가 가지고 있는 구조적인 한계점을 살펴본다.
이를 위해서 두 개의 hypothesis를 제시한다.
1. Transformers는 multi-step compositional reasoning을 linearized path matching으로 reduce해서 해결한다.
2. backpropagation으로 인해, Transformer는 high-complexity compositional task를 푸는 데 구조적인 문제가 있다.
이를 보이기 위해서 compositional task를 computation graph로 바꾼 후 Transformer의 해결 가능성에 대해 탐구한다.
2. Measuring Limitations of Transformers in Compositional Tasks
Computation Graph Definition
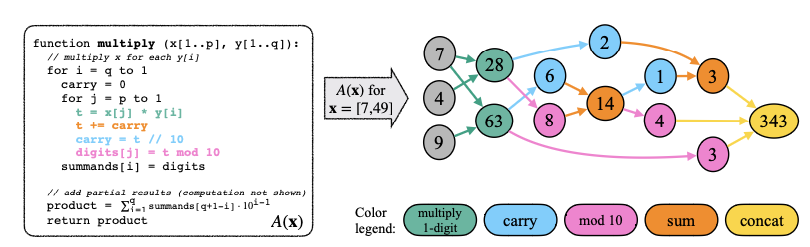
위는 두 수의 곱셈을 알고리즘화 한 것이다. computational graph로 표현되어 있고, 각 node는 하나의 숫자를 포함한다. 각 edge를 한 번 거칠 때마다 간단한 연산을 한 번씩 거쳐 결과를 도출하는데, LM이 이런 알고리즘 $A$를 배우기 위해서는 위 함수 $G_{A(x)}$를 linearize할 수 있어야 할 것이다. 이는 autoregressive model에서는 topological ordering의 형태가 되어야 한다.
Quantifying Compositional Complexity using Graph Metrics
알고리즘 $A$의 그래프 형태 representation을 이용하면 몇 가지 metric을 만들 수 있다.
- reasoning depth: task를 해결하기 위해 필요한 가장 긴 multi-hop reasoning이다. graph의 maximum depth로 정의할 수 있다.
- reasoning width: 한꺼번에 고려해야 하는 최대 수의 variable이다. 여기서는 root에서 vertex까지의 거리의 최빈값으로 계산했다.
- average paralellism
3. Testing the Limits of Transformer: Empirical Evidence
여기서는 LLM 중 5종류: GPT3, ChatGPT(GPT-3.5), GPT4, FlanT5, LLaMa를 사용하여 zero-shot, few-shot, finetuning에서의 결과를 비교하였다. computation graph를 만들기 위해 scratchpad라는 방법을 사용하였는데, 아래 Figure를 보면 쉽게 이해할 수 있다.

즉, scratchpad는 computation graph를 text로 표현할 수 있도록 하는 방법이다.
Zero-shot, Few-shot and Finetuning Results
- Limits of Transformers in zero- and few-shot settings
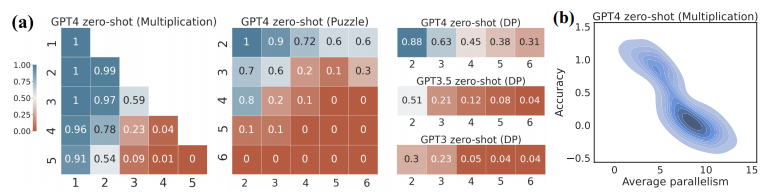
Figure 3 (a)의 각 axis는 problem size를 의미한다. 즉, (5, 5)는 5자리 수 간의 곱셈을 의미한다. Einstein's Puzzle에서는 house와 attribute의 개수이다. (b)는 parallelism에 따른 accuracy를 보여준다. negative correlation이 존재하여 parallelism의 개수가 늘어날 수록 accuracy가 떨어지는 것을 볼 수 있다.

이러한 경향성은 다른 task에서도 이어진다.

task complexity가 커질수록 accuracy가 현저하게 감소하는 것은 비단 GPT4만의 문제는 아니고, Transformer architecture를 쓰는 모든 LLM에서 나타난다.
- Limits of Transformers with QA training
위와 같은 결과는 task-specific한 data를 학습하지 못한 탓에 potential을 충분히 발휘하지 못해 발생한 문제로 생각할 수 있다. 이를 위해 multiplication problem에서 1자리-1자리 연산부터 4자리-2자리 연산까지 1.8M pair를 학습시키고, puzzle은 2x2부터 4x4까지 142K pair, DP taks에서는 length가 5인 seq까지 41K pair를 학습시킨 뒤 결과를 관찰했다.
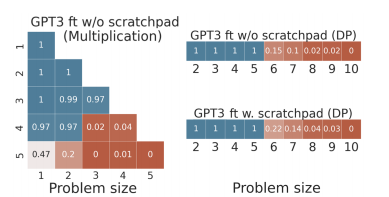

위 Figure 6과 Figure 7은 이렇게 finetuning한 GPT3의 multi-digit multiplication task에서의 결과를 보여준다. 4자리-2자리 연산, 3자리-3자리 연산까지는 괜찮은 결과를 내지만 4자리-3자리 연산부터는 정확도가 급격히 떨어진다. 이는 학습 과정에서 보지 못했던 out-of-distribution(OOD) 데이터에 대해 task를 generalization하지 못했음을 보여주는 결과이다.
연구자들은 tokenization의 문제일 것으로 생각하여 각각의 digit을 token으로 대체해 보았지만, 그래도 정확도는 크게 향상되지 않았다.
in-domain data에 대해서는 꽤 괜찮은 결과를 낸지만, OOD에 대해서 결과를 내지 못한다는 사실은 systemic problem-solving capability가 나타나지 않았음을 방증하는 결과이다.
- Limits of Transformers with explicit scratchpad training
모델이 scratchpad를 이용해서 computational operation을 수행할 수 있는지 확인한다. 먼저 GPT3를 scratchpad를 이용할 수 있도록 모든 task에 대해서 finetuning한다.

이 경우에도 결과는 별반 다르지 않아서, in-domain에서는 좋은 결과를 보여주지만 OOD에서는 완전히 fail한다.
이러한 결과들은 Transformer의 autoregressive한 특성이 task를 완전히 이해하고 해석하여 결과를 내놓는 것이 아니라, 단편적이고 greedy하게 text를 generate하는 데 그친다는 점을 시사한다. 이는 문제를 sequential하게 해석하지 못하도록 만든다.
Breaking Down Successes and Failures of Transformers
- Information Gain Explains Where Transformer Partially Excel
Transformer들은 전체적인 답변이 잘못된 경우에도 일부를 맞추는 경우가 있었다. 예컨대, 결과의 마지막 한 자리는 각 input의 첫 번째 자리와 highly correlated된 것을 볼 수 있었다. 이는 Transformer가 multi-hop reasoning을 하지 않고 입력값과 결과값이 directly mapping되는 경우에는 가짜 패턴을 만들어 학습하는 것임을 보여준다.
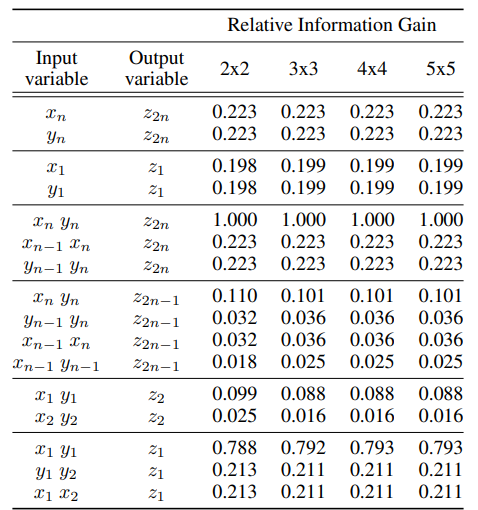
Table 1은 n자리 수인 x와 y를 input으로 넣었을 떄 결과와의 RIG를 보여준다. n이 least significant digit인데, $x_n y_n$과 $z_{2n}$의 correlation을 포착하고 있음을 알 수 있다.
- Transformers Reduce Multi-Step Compositional Reasoning into Linearized Subgraph Matching
이번에는 unseen data에 대한 model의 correct prediction이 underlying algorithm을 학습한 것인지, 아니면 단순히 비슷한 training example을 학습한 것인지에 대해 확인한다. 이를 확인하기 위해 training data에서 나타났던 partial computation을 사용하는 경우가 얼마나 되는지를 계산한다.
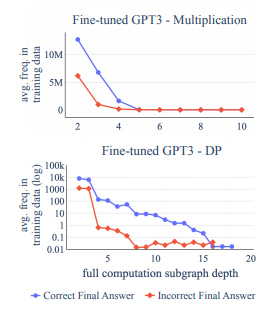
이를 측정하는 방법은 다음과 같다: 모델이 만든 computation graph $\hat G_{A(x)}$에 대해서 이 graph의 각 node들을 기준으로 그 ancestor들을 포함하는 subgraph를 만들 수 있다. 이 subgraph가 training에서 나타났으면 이 subgraph는 관측된 것으로 평가한다.
Figure 9를 보면, 가로 axis는 depth를 의미한다. depth가 깊어질수록 seen일 frequency가 현저하게 감소했다. 붉은 선은 final answer가 incorrect한 경우의 frequency를 나타낸 것이고, 파란 선은 correct final answer의 경우의 frequency를 나타낸 것이다. 확실하게도 correct한 answer를 얻은 경우 full computation subgraph가 training data에 있는 경우가 더 많았다.
즉, 이는 모델이 pattern matching 방식으로 문제를 풀고 있음을 의미하고, 이는 왜 in-domain의 낮은 complexity 문제에서 좋은 성능을 보이다가 complexity가 올라가거나 OOD가 되면 성능이 대폭 하락하는지를 설명한다.
> 추가 설명
algorithm $A(x)$에 대한 model generated compuation graph $\hat G_{A(x)}$에서 each node $v \in \hat V$가 얼마나 training 과정에서 나타났는지를 확인해야 한다. $v$'s full computation을 $v$를 포함한 모든 ancestor들로 이루어진 subgraph로 정의하고 $FC_{ \hat G_{A(x)}}(v)$로 표기한다. $FC_{\hat G_{A(x)}}(v)$ 는 training 과정에서 본 $FC_{\hat G_{A(x')}}(w)$와 유사할 때 관측된 것으로 평가하고, 이때의 depth는 $w$를 기준으로 계산한다.
* 어떤 경우가 유사한 것인지는 논문에 나와 있지 않다.
- What Types of Errors do Transformers Make at Different Reasoning Depths?
각각의 depth에서 Transformer가 어떤 error를 겪는지 확인한다. 여기서 error는 총 세 종류로 구분한다.
- fully correct: $v$와 ancestor가 correct value를 가지고 있고 올바른 computation으로 derive된 경우
- local error: parents node는 모두 올바른 값을 가지고 있지만, $v$가 잘못된 계산을 한 경우
- propagation error: $v$는 올바른 computation으로 derive되었지만 parents 중 일부가 잘못된 값을 가진 경우
- restoration error: 정답은 올바르지만 잘못된 계산으로 유도된 경우
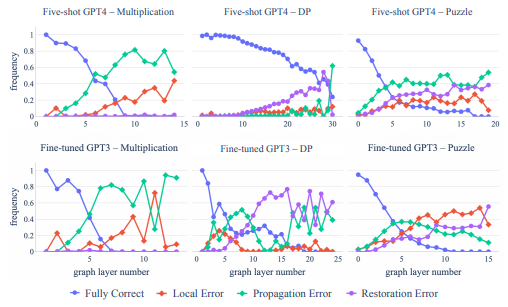
Figure 10은 finetuned GPT4와 scratchpad로 finetuned GPT3의 결과를 보여준다. 모든 경우에서, fully correct의 비율은 높지만 layer가 높아지면서 급격하게 떨어져 0으로 수렴한다. 보통 propagation error의 비율이 제일 높은데, 이는 모델이 single-step reasoning은 잘 하지만, 이는 memorization에 의한 것이고, overall correct reasoning을 하지는 못한다는 것을 의미한다.
DP와 Puzzle task에서는 correct도 높고 restoration error도 높은데, 이는 memorization으로 결과를 내고 있음을 의미한다.
4. Error Propagations: The Theoretical Limits
여기서는 Transformer가 한정된 능력을 가지는 이유를 theoretical하게 풀어낸다. 본래 compositional task를 풀기 위한 algorithm은 동일한 함수를 여러 차피 iteration하여 사용한다. transformer는 이와 동일한 방식으로 동작하는 것이 아니라, 이러한 함수를 근사하는 방식으로 동작한다. 이 경우 문제가 커질 경우 correct answer에 도달할 확률을 계산한다.

Proposition 4.1은 D.1에서 증명된다. 이는 function $g$를 근사하는 $\hat g$의 개수가 많아질수록, 원래 함수와 estimated 함수가 같지 않을 확률이 exponential하게 증가함을 보인다.

c가 $\epsilon$보다 훨씬 작을 경우 f의 estimation이 f와 다를 확률의 infimum은 1에 수렴한다. $g$가 low collision인 경우에 $c\ll \epsilon$이다.
5. Conclusion
- Collapsed Compositionality and Robustness Implication
Transformer architecture는 multi-step compositional task에 weakness를 가지고 있다. 그러나 어떤 task들은 compositionality를 가지고 있는 것처럼 보여도 그렇지 않아서 input에서 output으로 바로 matching할 수 있는 경우가 있다.
- Theoretical Findings and their Empirical Implications
본 논문에서 증명한 것처럼 compositional task에서는 단계가 증가할수록 incorrect할 확률이 1에 수렴하게 된다. 따라서 Transformer의 성능을 향상시키기 위해서는 다음 방법을 제안한다:
1. Transformer가 긴 추론을 하지 않고 정답에 도달하도록 구성
2. Transformer가 약간의 leniency를 가진 evaluation metric과 함께 compositional task에 구성
3. palnning moduel과 함께 구성
- Call for Broad Participation to Investigate Limiations
이 논문은 Transformer가 compositional operation을 수행하지 못하도록 하는 fundamental limitation에 대해 다루지만, 더 큰 모델에 대한 연구는 앞으로 해야 할 부분이라고 지적한다.
References
Footnotes
'DL·ML' 카테고리의 다른 글
| [Paper Review] Emerging Properties in Self-Supervised Vision Transformers (1) | 2024.02.06 |
|---|---|
| LLaMa2(GPT3) 사용기와 에러 정리 (1) | 2023.11.30 |
| TPU란 무엇인가? (1) | 2023.11.10 |
| [GNN] GNN Model (0) | 2023.11.07 |
| [DL] RLHF (Reinforcement Learning from Human Feedback) (0) | 2023.11.02 |