적률생성함수(Moment Generating Function, MGF)

적률(Moment)란 Random Variable X의 n승의 expectation을 의미한다.

예를 들어 X의 1차 적률은 E(X), 2차 적률은 E(X^2) 이런 식이다.

 

이런 적률을 생성하는 함수로서, 다음과 같다.

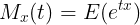
이 적률생성함수를 n번 미분하여 t=0을 대입하면 X의 n차 적률을 구할 수 있다.

증명

e^(tx)는 테일러 전개에 의해 다음과 같이 표현될 수 있다.

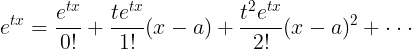
a=0을 대입하면 다음과 같다.(매클로린 급수)

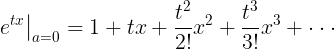
양변의 expectation은 다음과 같다.

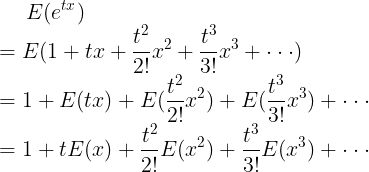
이 식의 양변을 n번 미분하고 t=0을 대입하면 적률을 구할 수 있다. 다음 예를 보자.

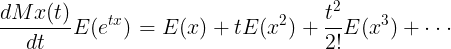
위와 같이 한 번 미분한 식에 t=0을 대입하면,

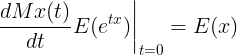
이를 일반화하면 다음과 같다.

 

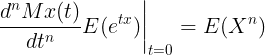
Continuous PDF의 경우

적분으로 expectation을 구할 수 있으므로 다음과 같이 구한다.

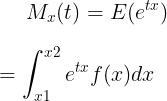
만약 normally distributed 이면,

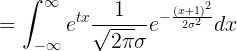
위와 같다.